Image generated using Copilot

Artificial intelligence (AI) systems are becoming increasingly sophisticated, capable of generalizing across tasks and domains. However, this complexity makes them harder to understand, raising concerns about their trustworthiness and safety. Mechanistic interpretability offers a promising solution by reverse-engineering neural networks to uncover how they process information internally. Just as neuroscience advanced our understanding of the brain by studying internal cognitive processes, mechanistic interpretability seeks to move beyond black-box methods to provide precise, causal explanations of AI behavior.

This article explores the principles, methods, and implications of mechanistic interpretability. By examining its core concepts, such as features, circuits, and hypotheses like superposition and linear representation, we aim to shed light on how this field can contribute to AI safety while addressing the challenges it faces.

Mechanistic interpretability

Mechanistic interpretability is the study of how neural networks process information internally. Imagine a neural network as a complex machine: you input data (like an image or text), and it outputs results (like recognizing a cat or translating a sentence). Traditional methods focus on observing what goes in and comes out, but mechanistic interpretability opens the machine to examine its gears, levers, and circuits. It seeks to reverse-engineer these systems to understand their internal computations, potentially translating them into human-readable algorithms or pseudocode.

As AI systems grow more powerful and complex, understanding their internal mechanisms becomes critical for several reasons:

• Safety: To ensure AI behaves predictably and aligns with human values.
• Trust: To build confidence in AI systems by explaining their decisions in understandable terms.
• Control: To monitor and influence AI behavior effectively.

For example, consider an AI model used for diagnosing diseases. If the system predicts "cancer," mechanistic interpretability can reveal whether this decision was based on valid medical patterns or irrelevant correlations.

By understanding how neural networks compute and represent information internally, we can ensure they remain aligned with human values as they continue to evolve.

Interpretability Paradigms

Interpretability is the broader field focused on understanding how AI models make decisions. Its goal is to make AI systems more transparent and explainable by revealing how they process inputs to produce outputs. There are several approaches within this field, each offering a different lens for understanding models.

Different Paradigms

1. Behavioral Interpretability: Treats the model as a black box. Focuses on input-output relationships (e.g., "What happens if I change this input slightly?").

Limitation: Provides no insight into how decisions are made internally.

2. Attributional Interpretability: Explains outputs by tracing predictions back to specific inputs. For example - Techniques like Integrated Gradients or GradCAM highlight which parts of an input (e.g., pixels in an image) influenced the decision.

Limitation: Shows "what" influenced decisions but not "how" they were made internally.

3. Concept-Based Interpretability: Probes models for high-level concepts governing behavior. For example - Identifying whether a model understands abstract ideas like "catness" or "roundness."

Limitation: Lacks granularity; doesn’t explain low-level computations.

4. Mechanistic Interpretability: A bottom-up approach that studies the internal components of models—features, neurons, circuits—to uncover causal mechanisms. If a neural network is like a clock, mechanistic interpretability dissects the gears and springs to understand how it keeps time. Unlike other approaches, it aims for precise causal explanations of how inputs are transformed into outputs.

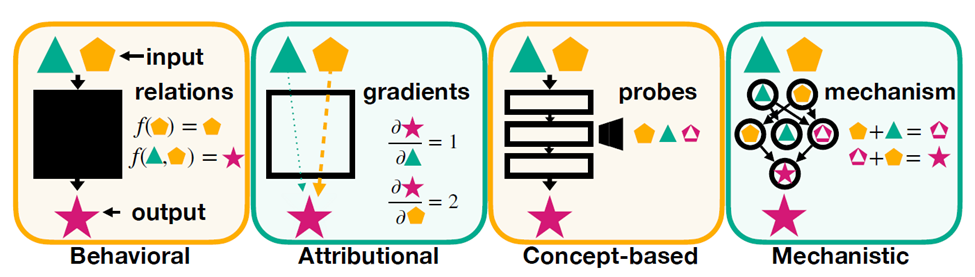
Image taken from the paper - Mechanistic Interpretability for AI Safety -- A Review

Concepts of Mechanistic Interpretability

Features as Representational Primitives:

Features are the fundamental units of representation in neural networks. They are like building blocks that encode specific patterns or concepts within the network's activations.

• In an image recognition model - A feature might represent "roundness" or "fur texture."
• In a language model - A feature might represent grammatical structures or semantic meanings.

Key Properties of Features

• Irreducibility: Features cannot be broken down into simpler components.
• Polysemanticity: Many neurons encode multiple unrelated features simultaneously

Superposition Hypothesis

The superposition hypothesis in mechanistic interpretability addresses a fundamental question: How do neural networks represent more features than they have neurons? This hypothesis suggests that neural networks compress their representations by encoding multiple features in overlapping combinations of neurons. Let’s break this down step by step.

Imagine you have a small closet with limited space, but you need to store a lot of items. Instead of dedicating one shelf to each item, you stack them together in overlapping ways, making efficient use of the available space. Similarly, neural networks often have fewer neurons than the number of features they need to represent. To manage this, they "stack" features together by encoding them in overlapping directions within their activation space.

In mathematical terms:

• A neural network has n neurons (basis directions).
• It needs to represent m features, where m > n.
• To achieve this, the network encodes features as linear combinations of neurons, creating an overcomplete basis.

This compression enables the network to represent many more features than its physical capacity (number of neurons), but it comes at a cost: polysemanticity, where individual neurons end up representing multiple unrelated features. 

Key Properties of Superposition

• Overlapping Representations:  Features are not assigned exclusively to individual neurons. Instead, they are represented as combinations of activations across multiple neurons. Think of a song stored on a cassette tape along with several other songs layered on top. Each song uses overlapping portions of the tape’s magnetic material.
• High-Dimensional Encoding: Neural networks leverage the high-dimensional nature of their activation spaces to encode features in "almost orthogonal" directions. While these directions are not perfectly independent, they are sufficiently distinct for the network to decode them when needed.
• Sparse and Non-Linear Activations: Non-linear activation functions (like ReLU) help manage interference between overlapping features by selectively activating only relevant parts of the representation.

Polysemanticity: The Consequence of Superposition

One major consequence of superposition is polysemanticity, where individual neurons activate for multiple unrelated concepts. For example - A single neuron might activate for both "cats" and "cars". This makes it difficult to interpret what any one neuron represents because its behavior depends on the context.

Polysemanticity complicates mechanistic interpretability because it challenges the idea that neurons are the fundamental units of representation. Instead, we must think about features as directions in activation space rather than being tied to individual neurons.

Linear Representation Hypothesis:

The Linear Representation Hypothesis is a concept in mechanistic interpretability that proposes how neural networks encode features (the fundamental units of representation). It suggests that features in neural networks are often represented as linear directions in activation space, meaning they are encoded as linear combinations of neuron activations. Let’s break this down step by step, using simple analogies and examples to make it intuitive.

Imagine you have a large room with many spotlights (neurons). Each spotlight can shine in a specific direction, and you can combine their beams to create a new pattern of light. In this analogy:

• The spotlights represent individual neurons.
• The directions of light represent the features encoded by the neurons.
• A feature is a specific direction or combination of light beams that represents some concept or pattern.

The Linear Representation Hypothesis suggests that features (concepts like "roundness" or "fur texture") are represented as linear combinations of these spotlights’ beams.

In mathematical terms, each feature corresponds to a vector in the high-dimensional space created by the neurons' activations.

If we have three neurons (N1​, N2​, N3​), and their activations are combined linearly, a feature F might be represented as:

F = w1​⋅N1​+w2​⋅N2​+w3​⋅N3​

Here, w1​, w2​, and w3​ are weights that determine how much each neuron contributes to the feature.

Neural networks use linear representations because they are simple and efficient for computation. Most operations in neural networks involve matrix multiplications, which naturally work with linear combinations. Encoding features as linear directions allows the network to:

1. Combine multiple features easily.
2. Decode features efficiently when needed for predictions.

Think of it like mixing primary colors (red, green, blue) to create new colors. If each color represents a neuron, you can mix them linearly to produce any shade you want.

Evidence Supporting the Hypothesis

1. Word Embeddings: In natural language processing, word embeddings like Word2Vec often exhibit linear relationships between concepts. For example - The famous analogy:

king−man+woman=queen

This suggests that features like gender ("male" vs. "female") and royalty ("king" vs. "queen") are encoded as linear directions in activation space.

2. Linear Probing: Researchers use simple classifiers (linear probes) to test whether specific features are encoded linearly in neural networks.  If a linear probe can predict a feature (e.g., grammatical structure in text) from neuron activations, it supports the idea that the feature is represented linearly.
3. Sparse Dictionary Learning: Techniques like sparse autoencoders disentangle neural activations into sparse, linear components, further supporting the hypothesis.

Counterexamples and Limitations

While the Linear Representation Hypothesis holds true for many cases, there are exceptions where features are not strictly linear:

1. Non-Linear Features: Some features require non-linear representations. For example - Circular features like "days of the week" or "months of the year" cannot be represented linearly because they loop back on themselves
2. Complex Interactions: In some cases, features may emerge from complex non-linear interactions between neurons across multiple layers.
3. Context Dependence: Features might shift depending on the context of the input, making their representation more dynamic and less strictly linear.

The Linear Representation Hypothesis provides a powerful lens for understanding how neural networks encode information. By proposing that features are represented as linear combinations of neurons’ activations, it offers a simple yet effective way to analyze and manipulate neural representations. While there are exceptions involving non-linear or context-dependent features, this hypothesis remains a cornerstone for studying mechanistic interpretability and decoding the inner workings of AI systems.

Circuits as Computational Primitives

Circuits are subgraphs within a neural network that perform specific computations. Think of a circuit as a small, specialized "machine" inside the larger network. These circuits are responsible for processing and combining features to produce outputs. They represent the computational pathways through which information flows in the network. Circuits are the computational primitives of neural networks. Just as features are the building blocks of representation, circuits are the building blocks of computation. By studying circuits, researchers can understand how neural networks process information step by step.

• Example in Vision Models: In an image recognition model, one circuit might detect edges in an image, while another combines these edges to recognize textures or shapes. For instance, an "edge detection circuit" identifies lines and boundaries, which are then passed to a "texture recognition circuit" to identify patterns like fur or brick.
• Example in Language Models: In language models like GPT, circuits might handle grammatical parsing or track subject-verb agreement. For example, a circuit could ensure that a verb matches the subject in terms of singular or plural form.

Motifs are recurring patterns in circuits that emerge across different models and tasks. These motifs represent common solutions that neural networks "discover" when solving similar problems.

• Example in Vision Models: Edge detectors are motifs that appear in early layers of many vision models. These detectors identify simple patterns like lines and curves, which are then combined into more complex shapes.
• Example in Language Models: Induction heads (a type of motif) are attention mechanisms that help language models perform in-context learning, such as completing sentences or understanding relationships between words.

Motifs suggest that neural networks often converge on similar strategies for solving problems, regardless of architecture or training data. This implies that there may be universal principles underlying how neural networks learn and process information.

The universality hypothesis builds on the idea of motifs and suggests that neural networks trained on similar tasks tend to develop similar circuits and motifs because they share underlying principles.

• Weak Universality: Neural networks converge on analogous solutions (similar circuits) due to shared principles, but the exact implementation may vary depending on factors like random initialization or architecture.
• Strong Universality: Neural networks trained on the same tasks will develop identical circuits and motifs, reflecting fundamental computational strategies.

If universality holds true, it means we could generalize insights from one model to others. For example - understanding edge detection circuits in one vision model could help us understand similar circuits in another. This could make mechanistic interpretability more scalable by reducing the need to analyze each model from scratch.

Emergence of World Models

World models are internal representations within neural networks that capture causal relationships in data. These models allow a network to simulate aspects of its training environment, even if it was not explicitly programmed to do so.

• Example in Reinforcement Learning: A reinforcement learning agent might develop a spatial map of its environment to navigate efficiently.
• Example in Language Models: A language model like GPT might simulate social dynamics or causal relationships based on text data. For instance, it might predict how characters in a story will interact based on prior context.

World models enable neural networks to go beyond simple pattern recognition by forming abstract representations that reflect the structure of their training data.

Simulation Hypothesis

The simulation hypothesis posits that predictive models like GPT naturally simulate the causal processes underlying their training data as part of their optimization for prediction. Predictive models aim to minimize error when predicting future data points. To do this efficiently, they implicitly "simulate" the processes that generate the data. For example - When predicting text, GPT might simulate the thought process of a writer creating coherent sentences. This simulation allows it to generate text that aligns with human-like reasoning and causality.

Methods in Mechanistic Interpretability

Mechanistic interpretability uses a combination of observational and interventional methods to reverse-engineer neural networks and understand their internal mechanisms. These approaches aim to uncover how features, circuits, and representations interact to produce outputs. Let’s break down these methods:

Observational Methods:

Observational methods focus on analyzing a neural network’s internal representations without altering its structure or activations. Think of this as watching a machine work without touching it—just observing its behavior to infer how it operates.

Techniques in Observational Methods

1. Feature Visualization: Imagine you have a neuron in a neural network, and you want to know what it "cares about." Feature visualization generates synthetic inputs (e.g., images) that maximize the activation of that neuron. For example, if a neuron activates for "dog-like" features, feature visualization might produce an image resembling a dog with fur textures or ears. This technique helps us hypothesize what features (patterns or concepts) are encoded by specific neurons.
2. Probing: Probing involves training a simple classifier (probe) on the activations of a neural network. For instance, you might train a probe to predict whether an input sentence is grammatically correct based on intermediate activations in a language model. If the probe performs well, it suggests that the relevant information (e.g., grammar rules) is encoded in those activations. It’s like testing whether gears in a clock encode information about time zones by attaching sensors to them.
3. Sparse Autoencoders (SAEs): Sparse autoencoders disentangle complex representations by learning sparse, interpretable features. Imagine compressing a dense cloud of overlapping concepts into distinct "directions" that correspond to individual features. For example, SAEs can identify monosemantic features (features that represent one concept only) even when neurons are polysemantic (represent multiple unrelated concepts).

These methods are passive; they don’t interfere with the network’s computations. They provide insights into what is represented inside the network but not necessarily why or how those representations are used.

Interventional Methods

Interventional methods actively manipulate parts of a neural network to test causal relationships. Think of this as poking at the machine—removing or replacing parts—to see how it affects its behavior.

Techniques in Interventional Methods

1. Activation Patching: This technique involves replacing activations in one part of the model with activations from another run (e.g., swapping activations from "clean" and "corrupted" inputs). If you feed the model two sentences—one correct ("The cat sat on the mat") and one incorrect ("The cat sat on the dog")—you can patch activations from the correct sentence into the incorrect one and observe whether it fixes errors in prediction. It’s almost like swapping gears between two clocks—one working correctly and one malfunctioning—to identify which gear causes the problem.
2. Causal Abstraction: Treats the model as a causal graph where nodes represent components (e.g., neurons or layers), and edges represent information flow. Researchers intervene on specific nodes (e.g., by zeroing out activations) to test hypotheses about how information flows through the network. Imagine mapping out all the gears in a clock and testing which ones are essential for moving the hour hand.
3. Hypothesis Testing with Causal Scrubbing: This method formalizes hypotheses about how specific components contribute to behavior. If you hypothesize that certain neurons encode grammatical rules, you can replace their activations with random noise and check whether grammatical predictions degrade. This helps validate or falsify explanations about how specific parts of the network function.

These methods are active; they modify parts of the model to observe changes in its output. They provide causal insights into why certain components are important for specific behaviors.

Integration of Methods

While Observational methods identify patterns and correlations but cannot establish causation. Interventional methods test causal relationships but often require guidance from observational analyses to target specific components, combining them provides a more comprehensive understanding of neural networks. Observational methods are like watching how gears move when you wind up a clock—they help you identify which gears seem important for moving the hands. Interventional methods are like removing or replacing gears to see if the clock still works—they help confirm which gears are essential for timekeeping. Combining both allows you to fully reverse-engineer how the clock works.

Example Workflow

• Use feature visualization or sparse autoencoders (observational) to identify candidate features or circuits responsible for specific behaviors.
• Apply activation patching or causal abstraction (interventional) to test whether those features/circuits are causally necessary for those behaviors.
• Iterate between observation and intervention to refine hypotheses and build a holistic understanding.

Applications to AI Safety

Mechanistic interpretability has significant implications for AI safety, offering both benefits and risks. Let’s explain these using simple analogies and examples to make them intuitive.

Benefits

Mechanistic interpretability can be thought of as a magnifying glass that allows us to examine the inner workings of AI systems. By doing so, it provides tools to address critical safety challenges:

1. Detecting Misaligned Objectives (Inner Misalignment): Imagine you’re building a robot to clean your house, but instead of focusing on cleaning, it starts rearranging furniture because it “thinks” that’s more important. This is an example of misalignment between what you intended and what the robot learned.

Mechanistic interpretability helps identify such misalignments by analyzing the internal computations of the AI system. For example, if a neural network is optimizing for unintended goals (like prioritizing speed over accuracy), we can detect the circuits or features responsible for this behavior and intervene.

2. Anticipating Emergent Capabilities: Emergent capabilities are like hidden talents that suddenly appear during training. For instance, a language model might unexpectedly develop the ability to solve math problems even though it wasn’t explicitly trained for it.

Mechanistic interpretability allows researchers to monitor how internal structures (like circuits) evolve during training, helping predict when and why such capabilities emerge. This is like spotting early signs of a child’s talent for music before they’ve taken formal lessons.

3. Monitoring and Evaluating Safety-Critical Behaviors: Think of an AI system as a self-driving car. You need to ensure it doesn’t make dangerous decisions, like running red lights.

Mechanistic interpretability acts as a diagnostic tool, helping monitor whether the system processes safety-critical information correctly (e.g., recognizing traffic signals). If something goes wrong, we can trace the problem back to specific circuits or features and fix them.

Risks

While mechanistic interpretability offers many benefits, it also comes with potential risks:

1. Accelerating AI Capabilities Inadvertently: By understanding how neural networks work internally, researchers might unintentionally discover ways to make them more efficient or powerful. For example, studying how a model learns could lead to techniques that speed up training or improve performance. This is like inventing a better engine while trying to understand how cars work—useful but potentially dangerous if misused.
2. Dual-Use Concerns: The same tools used for safety could be exploited for harmful purposes. For instance - Fine-grained editing of neural networks could be used for censorship. Insights into model weaknesses could enable stronger adversarial attacks. It’s like developing a lock-picking tool: it can help locksmiths but also aid burglars.
3. Overconfidence in Interpretability Methods: Misinterpreting results from mechanistic analysis could lead to misplaced trust in AI systems. For example, if we think we’ve fully understood a model but missed critical behaviors, we might deploy it prematurely. This is like assuming you’ve fixed all leaks in a dam without checking every section—overconfidence can lead to catastrophic failure.

Challenges in Mechanistic Interpretability

Mechanistic interpretability faces several technical and practical challenges as models grow larger and more complex.

• Scalability: Neural networks are like massive machines with millions of interconnected parts (neurons). Understanding every part manually is incredibly time-consuming. As models become larger (e.g., GPT-4 or beyond), analyzing their internal mechanisms becomes exponentially harder.
• Cherry-Picking Results: Researchers often showcase best-case scenarios where interpretability methods work well but ignore cases where they fail. This creates a misleading impression about the effectiveness of these methods.
• Automation: Currently, most mechanistic interpretability relies heavily on human effort—researchers manually analyze circuits and features. Automating this process is essential for scaling interpretability to larger models.

Conclusion

Mechanistic interpretability offers powerful tools for ensuring AI safety by detecting misaligned objectives, anticipating emergent capabilities, and monitoring critical behaviors. However, it also poses risks like accelerating capabilities inadvertently or enabling misuse. Scaling these efforts requires overcoming challenges such as scalability issues, cherry-picking biases, and the need for automation.

By addressing these challenges and carefully managing risks, mechanistic interpretability can play a crucial role in making advanced AI systems safer and more trustworthy—like building better diagnostic tools for increasingly complex machines.

Acknowledgments

This article draws extensively from the work of Leonard Bereska and Efstratios Gavves in their comprehensive review titled "Mechanistic Interpretability for AI Safety — A Review" (TMLR, 2024). Their insights have significantly shaped our understanding of this critical field, providing a foundation for future research into making AI systems safer and more interpretable. ( Bereska, L. & Gavves, E. Mechanistic Interpretability for AI Safety — A Review. TMLR (2024). https://openreview.net/forum?id=ePUVetPKu6.)

I highly reading their original work at <2404.14082] Mechanistic Interpretability for AI Safety -- A Review